Behavior planning
Behavior planning
Finite state machine -> think about all cases that car make
Frenet coordinate -> More useful than cartesian coordinate because of car usually drive through curve
Behavior planning pesudo code
def transition_function(predictions, current_fsm_state, current_pose, cost_functions, weights): # only consider states which can be reached from current FSM state. possible_successor_states = successor_states(current_fsm_state) # keep track of the total cost of each state. costs = [] for state in possible_successor_states: # generate a rough idea of what trajectory we would # follow IF we chose this state. trajectory_for_state = generate_trajectory(state, current_pose, predictions) # calculate the "cost" associated with that trajectory. cost_for_state = 0 for i in range(len(cost_functions)) : # apply each cost function to the generated trajectory cost_function = cost_functions[i] cost_for_cost_function = cost_function(trajectory_for_state, predictions) # multiply the cost by the associated weight weight = weights[i] cost_for_state += weight * cost_for_cost_function costs.append({'state' : state, 'cost' : cost_for_state}) # Find the minimum cost state. best_next_state = None min_cost = 9999999 for i in range(len(possible_successor_states)): state = possible_successor_states[i] cost = costs[i] if cost < min_cost: min_cost = cost best_next_state = state return best_next_stateWe use sigmoid function to calculate cost.
And there are so many cost functions in each situation.

- Δd was the lateral distance between the goal lane and the final chosen lane, and Δs was the longitudinal distance.
There are so many factors we have to consider!
There are two ways of find route. One is discrete methods and the other is probabilistic methods.
I don’t know the relationship between A star and heuristic function. -> I found the reason. It doesn’t expand to route that are not necessary!
A* – Discrete , World – continuous ! It has difference !
Hybrid A * -> It can be used in continuous world but is not complete . It cant find the way even though it has a solution.
https://d17h27t6h515a5.cloudfront.net/topher/2017/July/595fe838_junior-the-stanford-entry-in-the-urban-challenge/junior-the-stanford-entry-in-the-urban-challenge.pdf
This articles are very helpful.
psudo hybrid A* code
def expand(state, goal): next_states = [] for delta in range(-35, 40, 5): # Create a trajectory with delta as the steering angle using # the bicycle model: # ---Begin bicycle model--- delta_rad = deg_to_rad(delta) omega = SPEED/LENGTH * tan(delta_rad) next_x = state.x + SPEED * cos(theta) next_y = state.y + SPEED * sin(theta) next_theta = normalize(state.theta + omega) # ---End bicycle model----- next_g = state.g + 1 next_f = next_g + heuristic(next_x, next_y, goal) # Create a new State object with all of the "next" values. state = State(next_x, next_y, next_theta, next_g, next_f) next_states.append(state) return next_states def search(grid, start, goal): # The opened array keeps track of the stack of States objects we are # searching through. opened = [] # 3D array of zeros with dimensions: # (NUM_THETA_CELLS, grid x size, grid y size). closed = [[[0 for x in range(grid[0])] for y in range(len(grid))] for cell in range(NUM_THETA_CELLS)] # 3D array with same dimensions. Will be filled with State() objects # to keep track of the path through the grid. came_from = [[[0 for x in range(grid[0])] for y in range(len(grid))] for cell in range(NUM_THETA_CELLS)] # Create new state object to start the search with. x = start.x y = start.y theta = start.theta g = 0 f = heuristic(start.x, start.y, goal) state = State(x, y, theta, 0, f) opened.append(state) # The range from 0 to 2pi has been discretized into NUM_THETA_CELLS cells. # Here, theta_to_stack_number returns the cell that theta belongs to. # Smaller thetas (close to 0 when normalized into the range from 0 to # 2pi) have lower stack numbers, and larger thetas (close to 2pi when # normalized) have larger stack numbers. stack_num = theta_to_stack_number(state.theta) closed[stack_num][index(state.x)][index(state.y)] = 1 # Store our starting state. For other states, we will store the previous # state in the path, but the starting state has no previous. came_from[stack_num][index(state.x)][index(state.y)] = state # While there are still states to explore: while opened: # Sort the states by f-value and start search using the state with the # lowest f-value. This is crucial to the A* algorithm; the f-value # improves search efficiency by indicating where to look first. opened.sort(key=lambda state:state.f) current = opened.pop(0) # Check if the x and y coordinates are in the same grid cell # as the goal. (Note: The idx function returns the grid index for # a given coordinate.) if (idx(current.x) == goal[0]) and (idx(current.y) == goal.y): # If so, the trajectory has reached the goal. return path # Otherwise, expand the current state to get a list of possible # next states. next_states = expand(current, goal) for next_s in next_states: # If we have expanded outside the grid, skip this next_s. if next_s is not in the grid: continue # Otherwise, check that we haven't already visited this cell and # that there is not an obstacle in the grid there. stack_num = theta_to_stack_number(next_s.theta) if closed[stack_num][idx(next_s.x)][idx(next_s.y)] == 0 and grid[idx(next_s.x)][idx(next_s.y)] == 0: # The state can be added to the opened stack. opened.append(next_s) # The stack_number, idx(next_s.x), idx(next_s.y) tuple # has now been visited, so it can be closed. closed[stack_num][idx(next_s.x)][idx(next_s.y)] = 1 # The next_s came from the current state, and is recorded. came_from[stack_num][idx(next_s.x)][idx(next_s.y)] = current

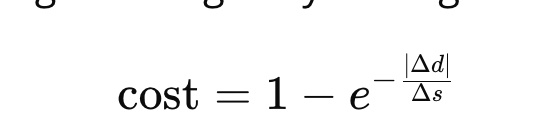

Leave a comment