Deeplearning

How Deep Learning Learns

What is a Neural Network?

• Studying neural networks means studying nonlinear models, which are essentially combinations of linear models and nonlinear functions.
• To understand neural networks, you must first understand the concepts of softmax and activation functions.
• Understanding how linear models work is key to understanding how to build and train nonlinear models.
• Before diving in, let’s define matrices in the context of deep learning. There are two main types:
  • Data matrices: collections of input data
  • Transformation matrices: used to map data into different dimensions or spaces
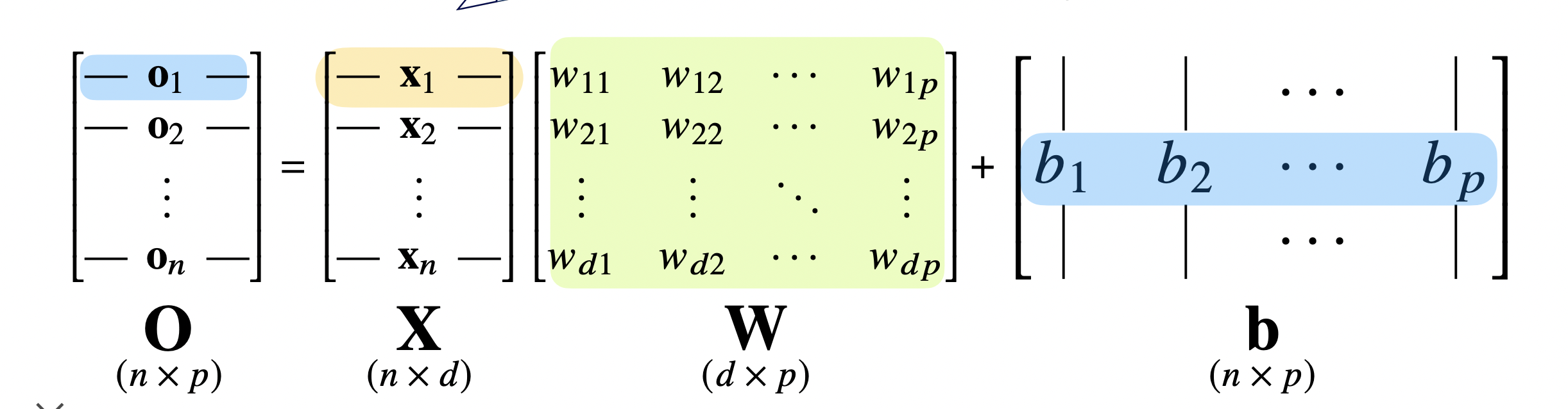
• In the image above:
  • X is the data matrix
  • W is the weight matrix
  • b is the bias matrix (each row has the same value)
  • After applying operations, the output vector’s dimension changes from d to p.
• This essentially means we build p linear models from d input features, allowing us to define a more complex function using p latent variables.

Softmax Operation

• The softmax function converts the model’s output into probabilities.
• It’s used in classification tasks to determine whether an input belongs to class k.
• In short, classification problems = linear model + softmax function.
• But why was softmax introduced?
  • For simple inference, one-hot vectors might suffice.
  • However, in general, outputs from linear models aren’t valid probability vectors. Softmax transforms them into proper probability distributions for classification.

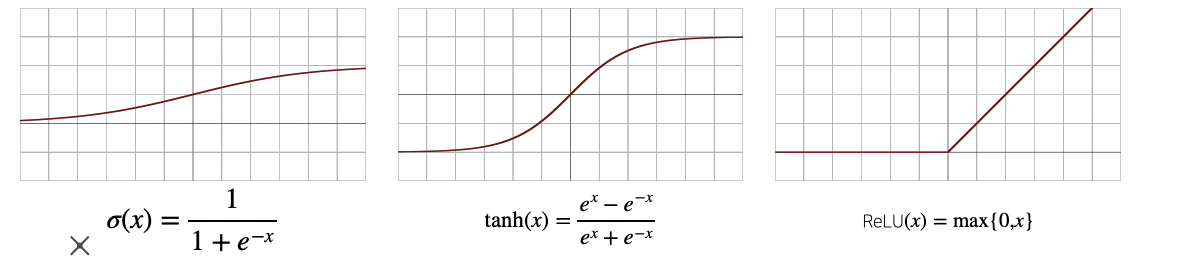
Activation Function

• Why do we need activation functions?
  • They serve as a trick to enable modeling of nonlinear functions.
• Activation functions are nonlinear functions applied to each element of the linear model’s output.
• They are applied element-wise, not to the entire vector at once.
• Inputs are typically real numbers (not vectors), and the outputs are also real numbers.
• Using activation functions, we can convert the output of a linear model into a nonlinear model.
• The most widely used activation function today is ReLU.

How Does Deep Learning Learn?

• Simply put, it involves repeatedly applying linear models and activation functions.
• Let’s understand this by looking at a two-layer neural network:
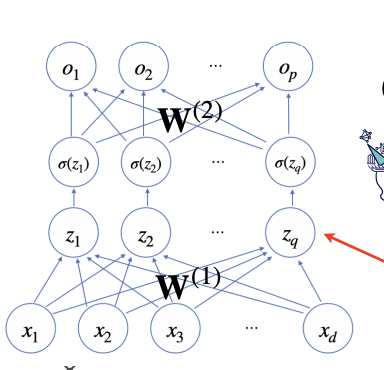
• For each element z in the matrix, apply an activation function: $\displaystyle\sum_{n=1} ^{\infty} z$
• Why not stop at two layers?
  • The more layers you stack, the fewer neurons are needed to approximate the target function — making the model more efficient.
• Forward propagation:
  • Takes input x and repeatedly applies linear models and composition functions.
• Backward propagation:
  • Applies gradient descent. You need to compute gradients of weights at each layer.
  • Use the derivatives of parameters at each layer to apply gradient descent to all elements in the weight matrices.
• In deep learning, each layer is computed sequentially, and you can’t skip more than one layer during the computation.
  • First, compute gradients at the top layer, then proceed layer by layer downward.