FFT

Fourier series

• Periodic signal을 periodic signal의 합으로 나타내자.

Fourier transform

• Fourier series의 확장버전(비주기함수에 대한 fourier series라 볼 수 있다. )

• 주기를 무한대로 볼때, aperiodic signal을 aperiodic signal의 합으로 나타내자.

• Fourier transform을 통해, 변환 전값과 변환 후 값이 1대1대응을 이룬다.

• 아이디어

주기신호의 주기를 무한대로 보내서 비주기신호로 보겠다 라는 아이디어

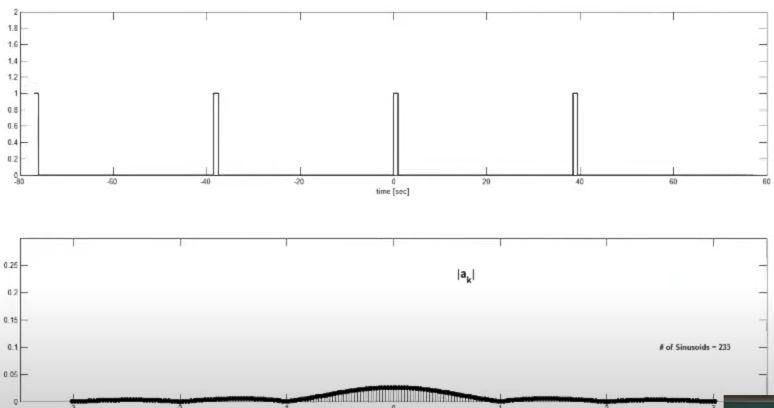
퓨리에 계수를 보니 주기가 늘어날수록 작아진다 당연히 T0를 무한대로 보내면 a_K는 0으로 수렴한다.

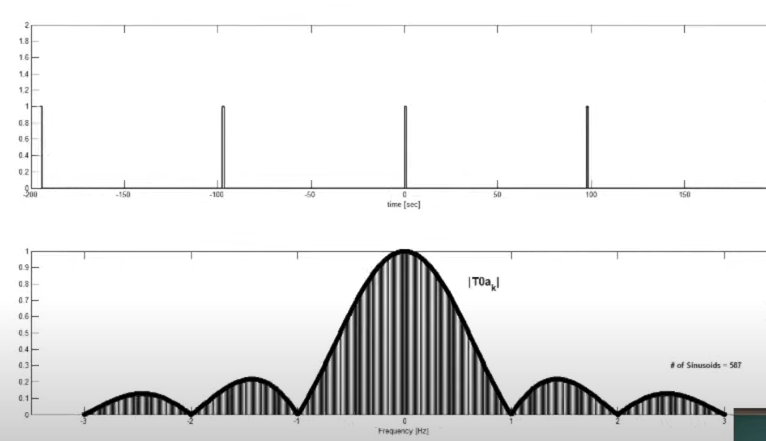
하지만, T0a_k 그래프를 보면, 주기가 무한대로 발산해도 값이 실수값을 가진다.

\[a_k = {\frac{1}{T_0} \int_\frac{-T_0}{2}^\frac{T_0}{2} \! x_{T_0} \mathrm{e}^{-jk\omega t}\, dt }\]

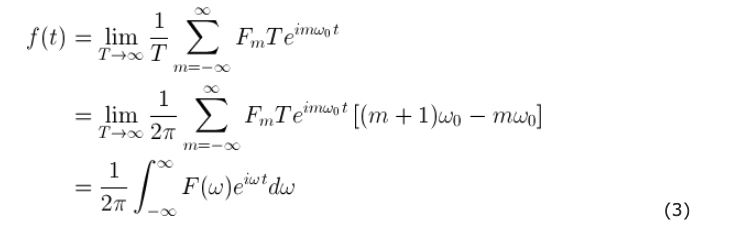
Derivation of FT and IFT

• 비주기 신호에 관한 퓨리에 시리즈가 어떻게 될지 관찰해보자

\[a_kT_0 = \lim_{T_0 \to \infty}{\int_\frac{-T_0}{2}^\frac{T_0}{2} \! x_{T_0}(t) \mathrm{e}^{-jk\omega_0 t}\, dt }\]

• 이때, 극한을 취하면 다음과 같이 나타날 수 있다.

\[{x_{T_0}(t) = x(t)} \\ {a_kT_0 = X(KW_0)} \\ KW_0 = w(=실수) \\ X(w) = \int_{-\infty}^{\infty} x(t)\mathrm{e}^{-j\omega t}\ dt\]

• x(t)를 가지고 X(w)를 만든다. 일대일 대응을 이루기 떄문에 역방향으로도 표현가능하다.

• 각각 내적을 해보면서 느린애도 내적해보고 빠른애도 내적해보고, 어떤 주파수와 닮았는지 확인하는 과정이다.

contribution(a_k)

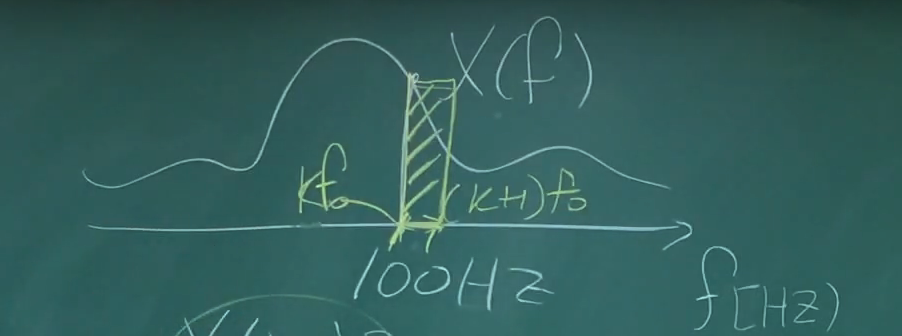
다음과 같은 주파수의 100hz의 contribution은 얼마인가?

바로 넓이 -> 밀도를 이야기하는것 , 마치 확률밀도함수 같은것 !!

//FT of delta function//

Discrete Time Fourier Series

\[x_{T_0}(t) = \displaystyle\sum_{k=-\infin}^{\infin}{a_k e^{jk\omega_0t}} \\ x_N[n] = \displaystyle\sum_{k=-\infin}^{\infin}{a_k e^{jk\frac{2\pi}{N}n}} \\\]

• 여기서 중요한것은, k = 1일때 , k = n + 1일때, 기저벡터가 일치한다는 것이다.

• basis가 반복이 되니까, 결국 실질적으로 구성되는 basis는 n개뿐이다. n주기를 가지고 반복된다

• 이번에는 ak를 구하기 위해서 각 기저벡터를 내적해보자.

\[\displaystyle\sum_{n=<N>}{X_N[n]e^{jr\frac{2\pi}{N}n}} = \displaystyle\sum_{n=<N>}\displaystyle\sum_{k=<N>}{a_k e^{jk\frac{2\pi}{N}n} e^{-jr\frac{2\pi}{N}n}} \\\]

• k = r일때만 값이 0 이 아니다. 따라서,

\[a_k = \frac{1}{N}{\sum_{n = <N>}x_n[n]{e}^{-jk\frac{2\pi}{N}n}\ }\]

Discrete Time Fourier Transform

• 그전과 똑같이 비주기 함수는 주기함수의 주기를 무한대로 발산시켰을때의 함수라고 보자.
• 주기를 늘리기전과 후의 결과값 비교!

\[a_kN ={\sum_{n = <N>}x_n[n]{e}^{-jk\frac{2\pi}{N}n}\ } \\ n -> \infty\\ x_n[n] = x[n]\\ a_kN = X(K\ohm_0)\\ k\ohm_0 -> 0부터 2\pi사이의 실수값 = \ohm \\ X(\ohm) = {\sum_{n = <N>}x[n]{e}^{-j\ohm n}\ }\]

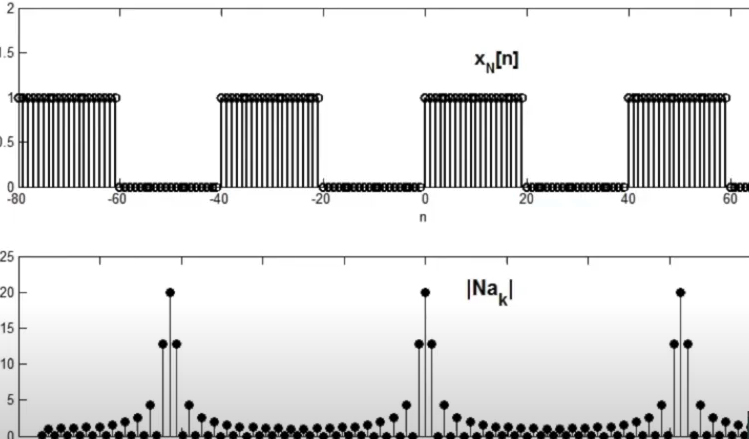
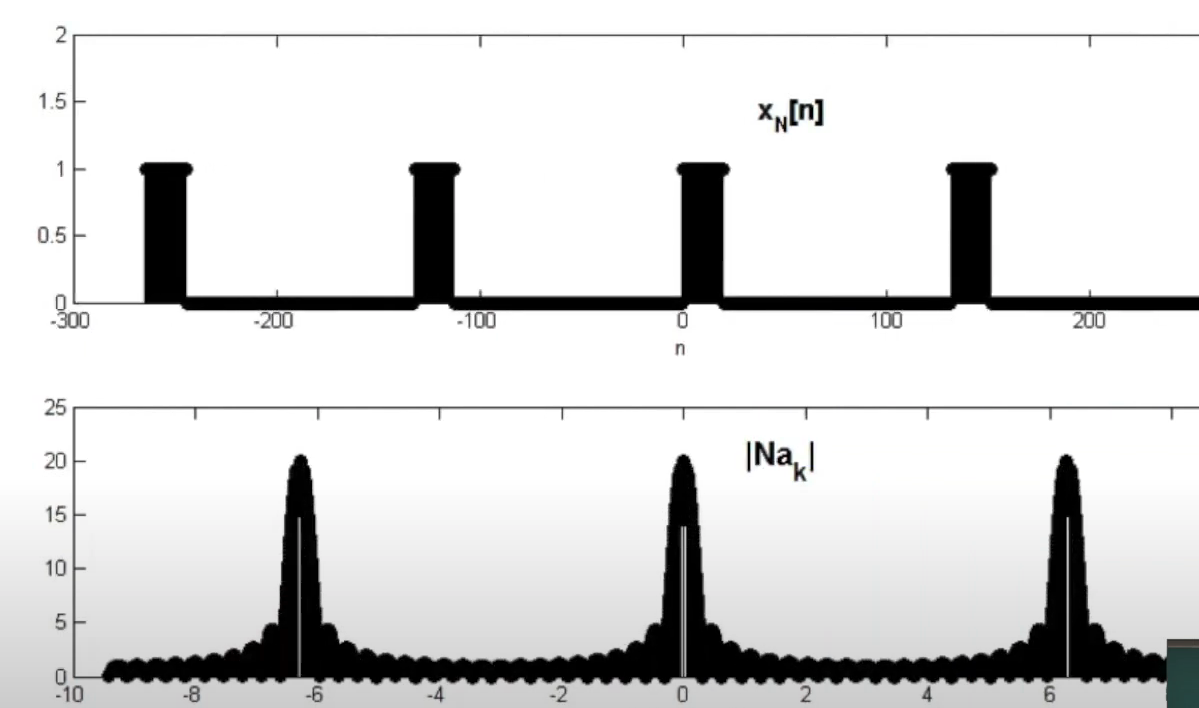
Discrete Fourier Transform

• 실제로 컴퓨터에서 써먹을 수 있다. (디지털 도메인에서 활용가능)
• discrete transform 해서 discrete 한값이 output으로 나온다. (CTFS, DTFS든 output이 연속적인 값이였다.)
• 정의 : 0 ~ N-1까지 값을 가지는 x[n]을 dtft한 다음 2pi/n간격으로 값을 뽑는다.(sampling과는 다르다.)

\[X_K=X(K\frac{2\pi}{N}) = {\sum_{n = <N>}x[n]{e}^{-j\ohm n}\ }\\\]

DFT matrix

\[X_K= {\sum_{n = 0}^{N-1}x[n]{e}^{-jk\frac{2\pi}{N}n}\ }\]

• k를 바꿔가면서 내적을 한다 -> 다음과 같이 행렬로 나타낸다

• 예시(3개의 데이터를 넣고, 3개의 값을 받는다.)

\[\begin{bmatrix} X_0 \\ X_1 \\ X_2 \end{bmatrix} = \begin{bmatrix} e^{-j0\frac{2\pi}{N}0}&e^{-j0\frac{2\pi}{N}1}&e^{-j0\frac{2\pi}{N}2} \\ e^{-j1\frac{2\pi}{N}0}&e^{-j1\frac{2\pi}{N}1}&e^{-j1\frac{2\pi}{N}2} \\ e^{-j2\frac{2\pi}{N}0}&e^{-j2\frac{2\pi}{N}1}&e^{-j2\frac{2\pi}{N}2} \end{bmatrix} \begin{bmatrix} x[0] \\ x[1] \\ x[2] \end{bmatrix}\]

• 
• 

• 

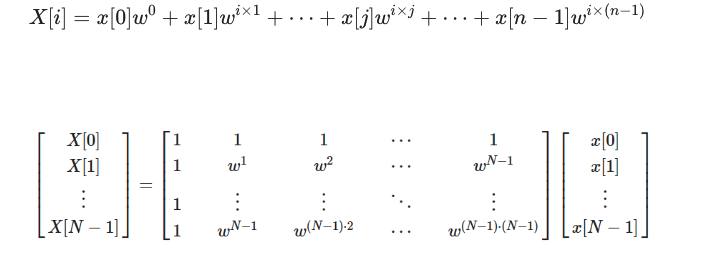
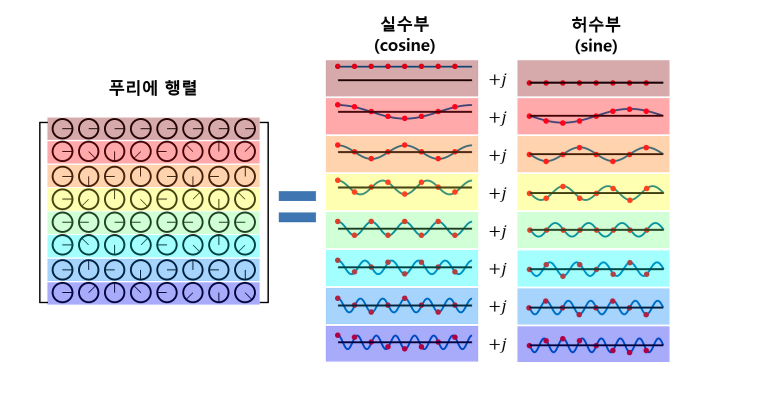
• Orthogonal -> orthonormal한 벡터를 column으로 가지고 있는 행렬
• unitary matrix로 만들면 장점이 있다. -> IDFT를 구하기 매우 쉽다. (복소수의conjugate 성질에 의해)

제한시간이 1초일 경우, N의범위에 따른 시간복잡도 선택

• N 의 범위가 500 인 경우
  • 시간 복잡도가 O(N^3) 이하인 알고리즘을 설계
• N 의 범위가 2,000 인 경우
  • 시간 복잡도가 O(N^2) 이하인 알고리즘을 설계
• N 의 범위가 100,000 인 경우
  • 시간 복잡도가 O(NlogN) 이하인 알고리즘을 설계
• N 의 범위가 10,000,000 인 경우
  • 시간 복잡도가 O(N) 이하인 알고리즘을 설계
• N 의 범위가 10,000,000,000 인 경우
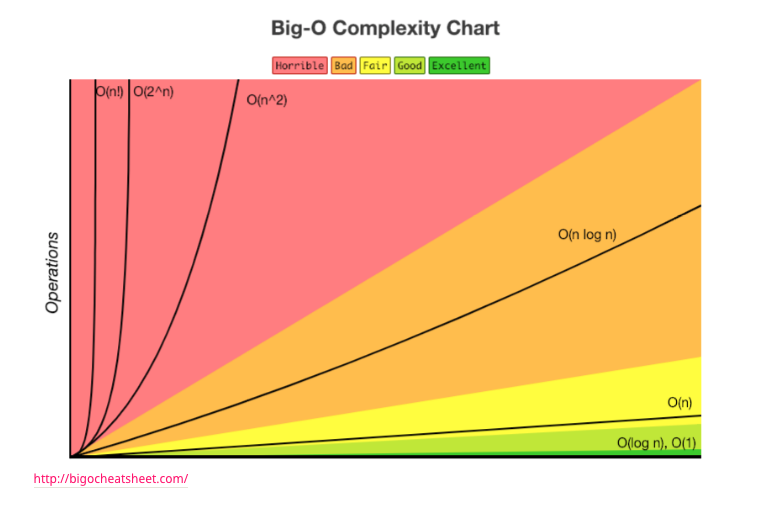
  • 시간 복잡도가 O(logN) 이하인 알고리즘을 설계

FFT

다항식 곱과 비슷하다.~

다항식곱은 계수만 작업해서 필요하다~~

시간복잡도 -> $d^2

일대일 대응이다 그림과 ~~

행렬로 쓰면 -> 역변환이 가능하다는 점이 장점

coefficiendt representation

value representation

magical ??

이렇게 시간복잡도를 줄이는 구나~~

PSD

• 신호의 크기를 제곱평균으로 표현한것

• 수학적인 의미에서 제곱평균은 파워를 의미한다….

• 주파수도메인에서 표현

• used to characterize random vibration signals

• used to characterize broadband random signals.

• a PSD has amplitude units of g2/Hz

• results in the real only spectrum of amplitude in g2.

• his amplitude value is then normalized to the frequency bin width to get units of g2/Hz.

  we get rid of the dependency on bin width so that we can compare vibration levels in signals of different lengths.(장점)

• FFT는 여러 성분의 정현파 진동 해석에 효과적이긴 하나 랜덤 진동에서는 PSD 분석이 효과적이다.

• 복소수 성분과 곱해서 진폭의 실수값 (g^2) 를 만들어주며 주파수 레졸루션 으로 나주어 준다 (g^2/Hz).-> 주파수 레졸루션에 대해서 비의존적이어서 다른 데이터의 개수를 가지는 신호의 진동 수준을 비교하기에 유용하다.

• 나이키스트 주파수 오천까지 보면 샘플수가 많을수록 (즉 샘플 시간이 길어질수록) FFT의 진폭이 크게 감소하게되는데 ( FFT의 bin width 가 줄어들기 때문) 반면에 PSD는 큰 변화가 없다. 게다가 FFT 결과는 2천 Hz 이후에는 샘플 개수에 따라 진폭이 급격히 변화하는데 PSD는 큰 변화가 없다. 즉 랜덤데이터 분석시에 PSD는 샘플 시간에 의존적이지 않으나 FFT는 의존적이다.

• As you see, the PSD of different signal lengths just fills in this area but the amplitude doesn’t change overall. The FFT amplitude however shifts down as the bandwidth is increased.

• 에너지 -> 제곱값

• 제곱을 해준다는것 자체가 양수로 만들어준다는것

• 주기적인 신호에 대해서는 에너지가 무한이 자동으로 되므로 의미가없다. 따라서, E/T가 의미가있어진다

• 비주기신호같은경우는 에너지가 의미가 있고, 에너지가 유한하다.

• 에너지 -> 파워 0

• 주기신호 -> 파워를 구하는게 의미있다

• 비주기신호 -> 에너지 구하는게 의미있다

• 주파수별로 어떤식읋 에너지분포

• 파워스펙트럼? 왜 덴시티라는 말이 붙냐면 , 적분하는 순간, 이 안에 얼마만큼의 파워가 들어가는지 알 수 있다. 하나의 밀도 형태

• 주기신호가 있으면 파워가 관심이 있어지고, psd가 가능해진다

• 비주기신호 -> 에너지 스펙트럴 덴시티가 된다

• 주기신호 -> 퓨리에 시리즈함

• 비주기신호 -> 퓨리에변환

• 왜 psd가 필요할까? 내가 원하는 구간에서의 주파수나 파워를 구할수있음

• orthogonality ->

• 주파수 분석을 했는데, 구간을 나누었어, `

• t-domain, f-domain 와리가리 해서 퓨리에 시리즈의 contribution으로, 파워를 구할 수 있다. 그래서, 특정 주파수의 들어있는 파워를 구할 수 있게된다…

• 퓨리에 시리즈와 퓨리에 변환은 주파수도메인과 타임도메인을 왔다갔다 하는것, 에너지나 파워자체는 변하지 않는다…

• 주파수를 구간별로, 내가 관심이 있는 주파수 구간으로 파워나 에너지를 구할 수 있다는게 핵심

• 어떤식으로 에너지와 파워가 분포가 되어있는지를 알아야 할떄가 있다. 그때가 언제인가? 이퀄라이져, 고주파의 비율과 저주파의 비율을 맞춘다…

• mass -> density, energy/power -> psd, esd 필요

• 주기적인 성부 -> 파워가 의미있다…

• 왜 psd는 샘플시간에 영향을 받지 않을까?? 그게 정말 궁금하네… ㅋㅋㅋ … ㅋㅋㅋ…

• 왜 g^2 / hz로 단위가 되는것일까? 정말 이해가 안되긴하네?

• fft에서의 contribution값 g는 도대체가 뭐야?

• 시간도메인에서 주파수도메인으로 진동을 변환할 때, g값에너지를 어떻게 처리할 것이냐? 그때, 왜 샘플링의 개수에 따라서 바뀌는거지?

• 문제는 샘플링 횟수, 샘플링 폭에 따라서 RMS값이 달라진다.

• 왜 fit 샘플링 횟수 많아지면은 ,….. 음 ? 값이 줄어들어??

  궁금한점

  • scipy, welch’s method를 이용할때의 차이점?